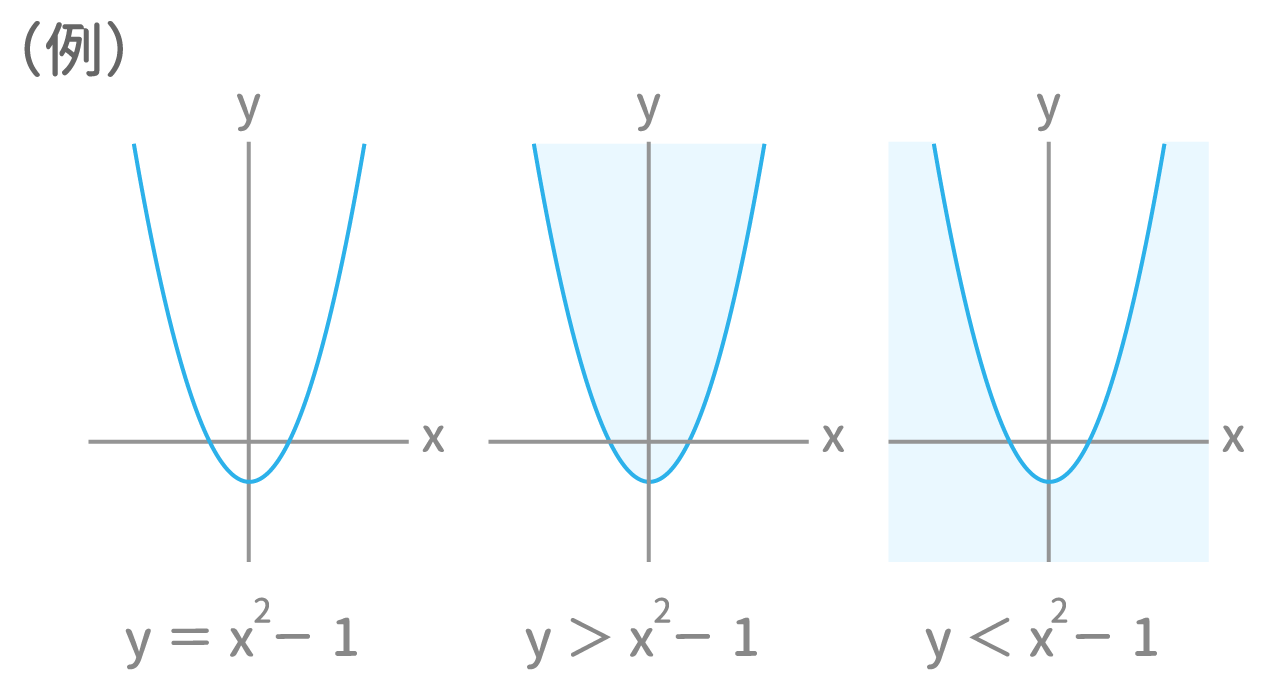
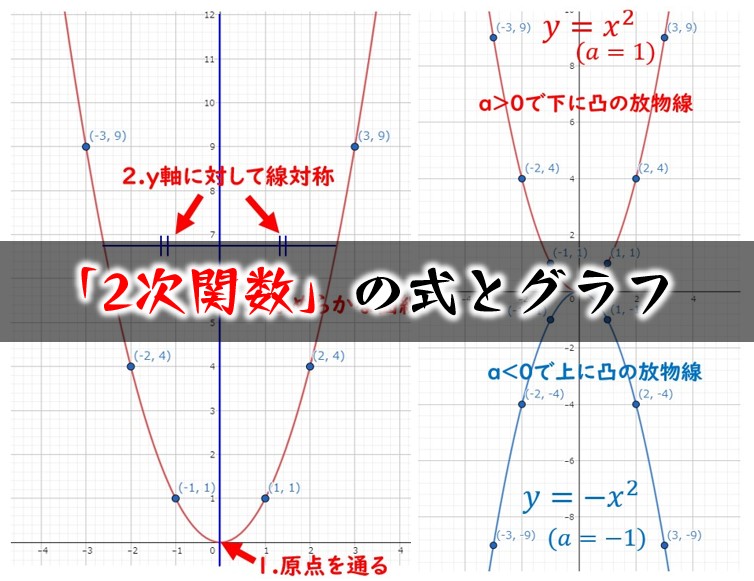
Y=x2乗のグラフ 958660
二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い
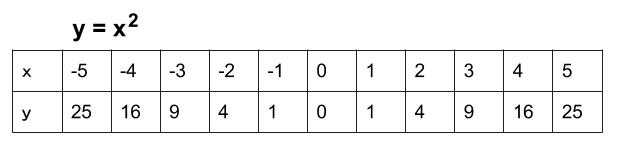
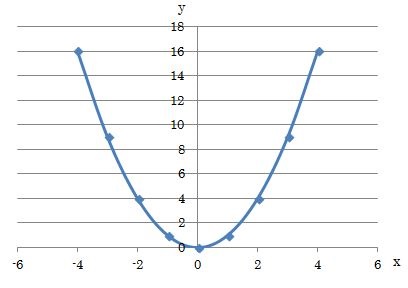
Y=ax2乗のグラフを書く手順 表を作る 座標を読み取って、グラフに書き込む 点をなめらかな線で結ぶ 完成! かず先生 では、この手順に従ってグラフを書いてみましょう。 次のグラフを書きなさい。 まずは、表を作ってみましょう。2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献 ・高橋『微分と積分2』§31定理36 (p67) 定理:2次同次関数の標準形 文献
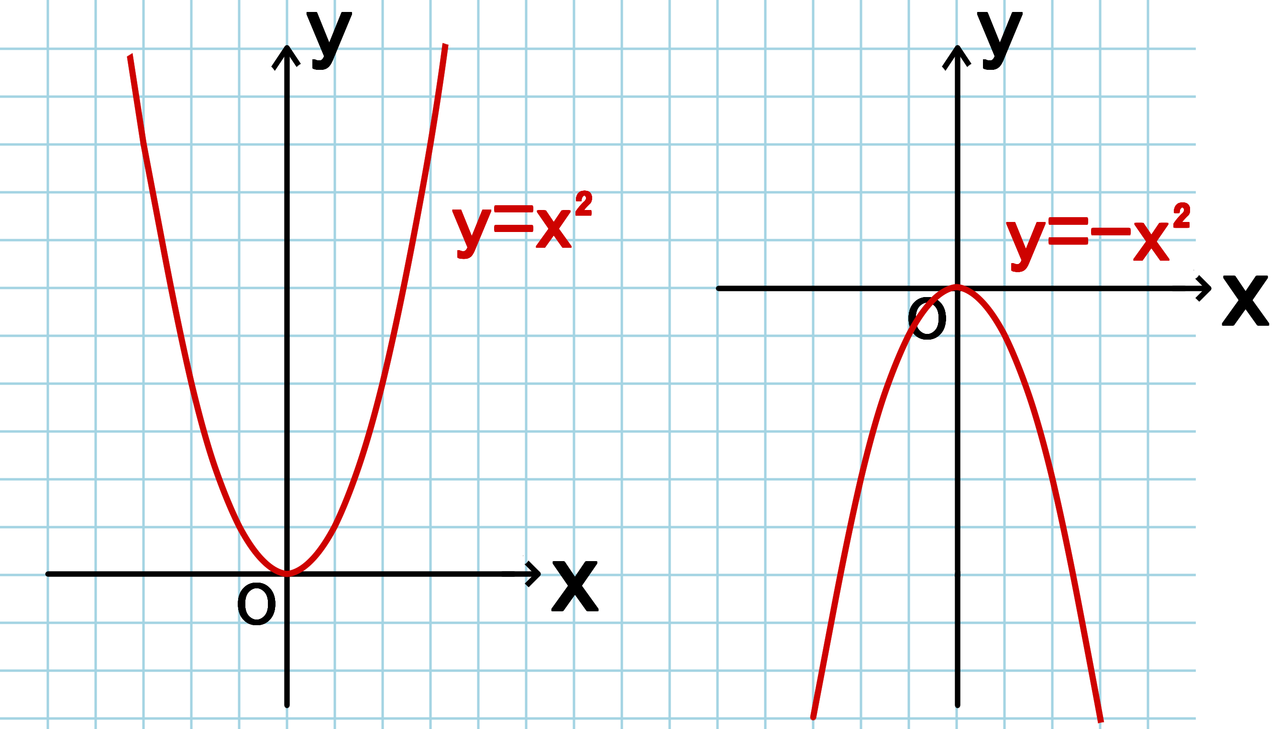
Y=x2乗のグラフ
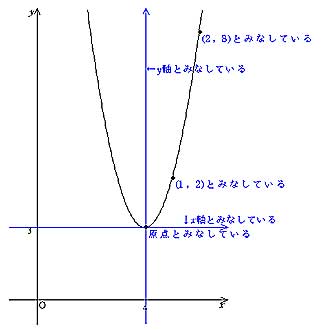
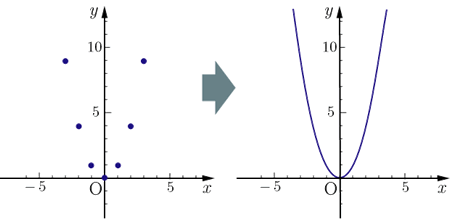
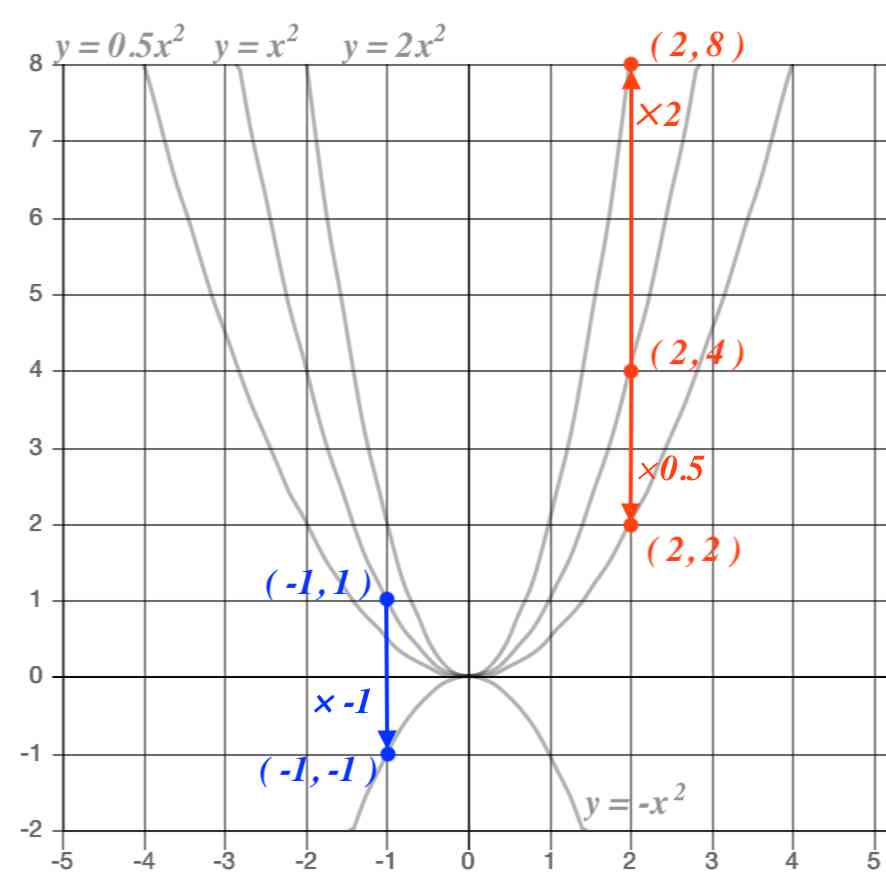
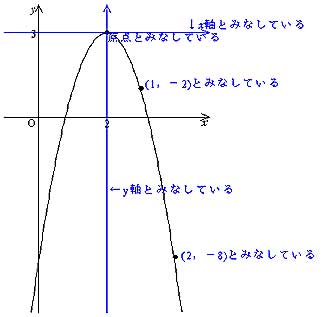
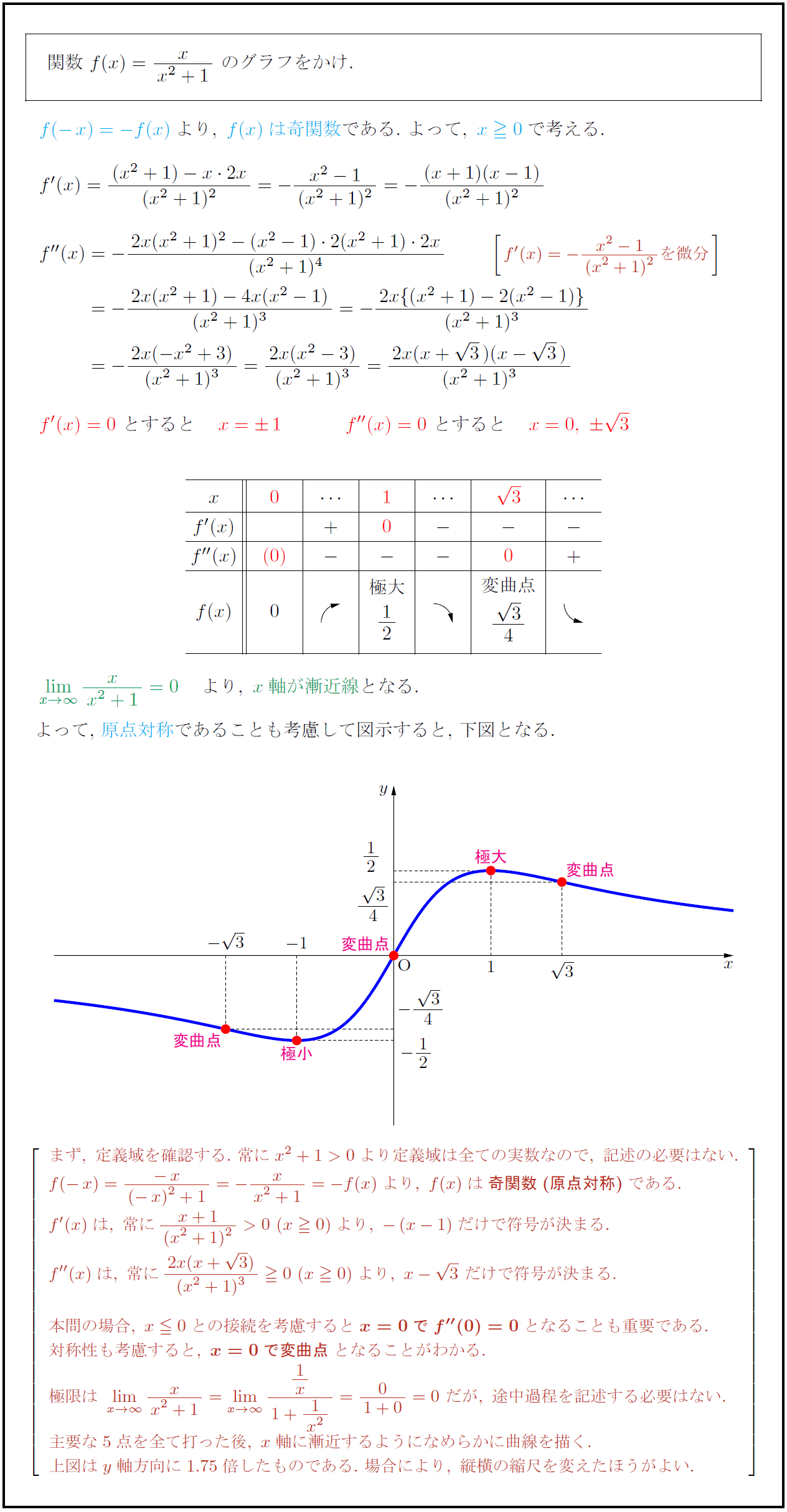
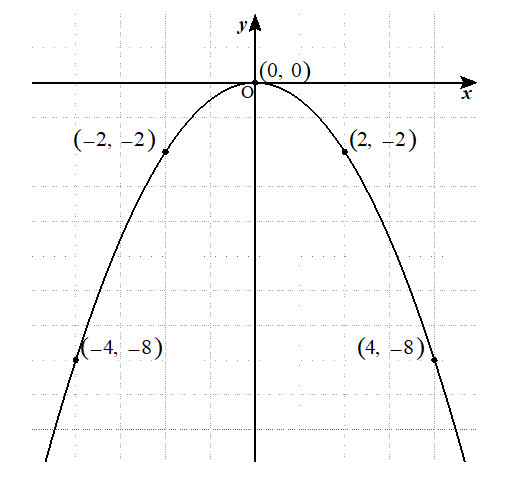
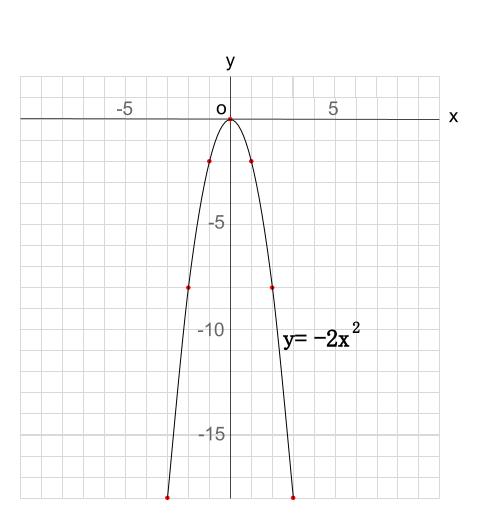
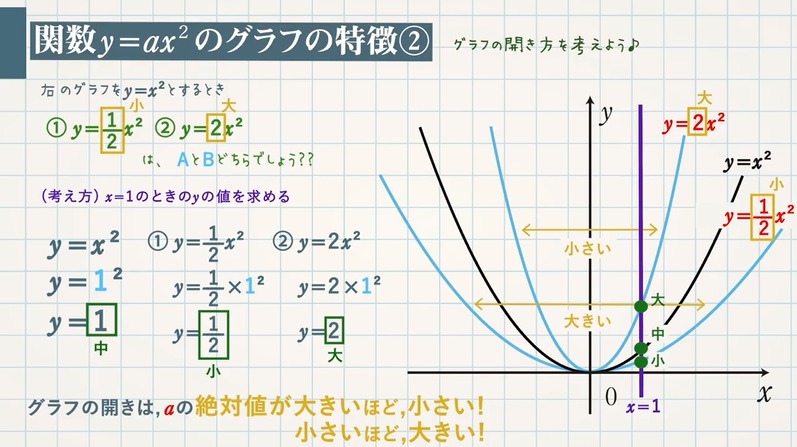
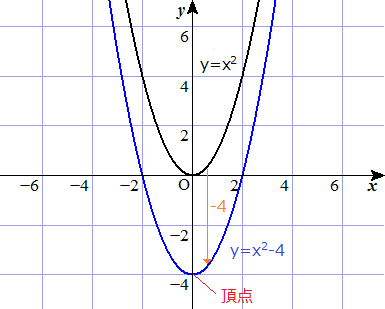
Y=x2乗のグラフ-グラフの書く時大事なのは ・頂点の座標 ・xが0の時のy ・yが0の時のx 今回の場合は ・式より頂点(1,0) ・x=0を代入してy=2 ・y=0を代入してx=1(頂点があるのでやらなくてもよし)Y=ax2 のグラフをかいてみましょう。aの値によって、グラフはどのようになるでしょうか。 y=x2 のグラフ(青色)も、y=2x2 のグラフ(緑色)も放物線になります。比例定数が大きいほうがグラフは細長くなります。なぜなら、x の値に対

中3数学 Y X2乗のグラフの変域 5分で学習 Youtube
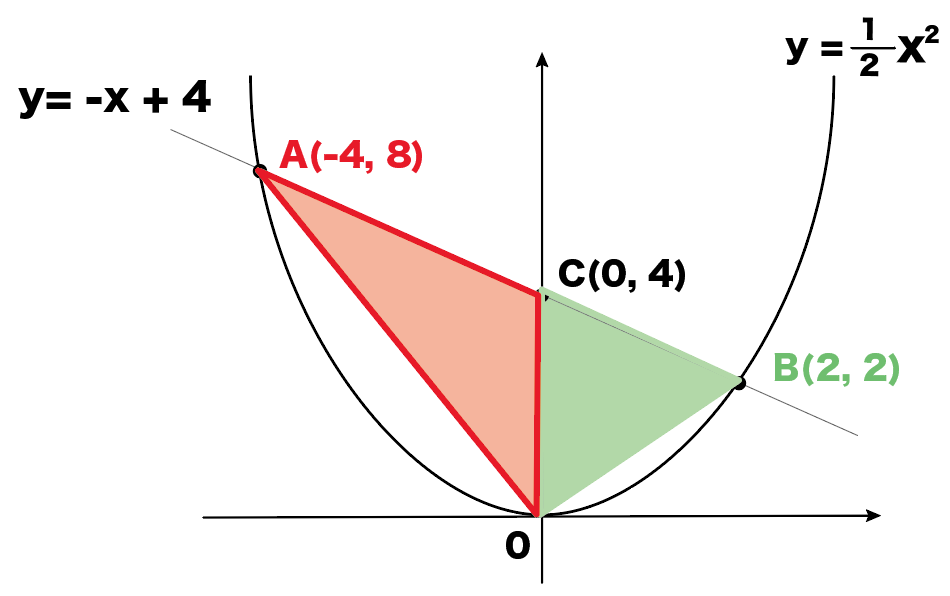
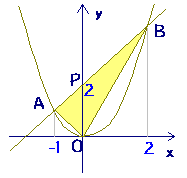
A,Bの座標が次のそれぞれの場合において、y=ax 2 のグラフが線分AB(両端を含む)と交わるようなaの値の範囲を求めよ。 A(2,1), B(2,8) A(4, 4), B(4, 8) A(3, 1), B(3, 9) 図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が中3数学。2乗に比例する関数 (y = ax²)。この a は「変化の割合」? xの値が「0から2まで」増加する? 分からん(ガクッ)倒れ込む中学生。立て、立つんだトォォォォ~ッ! オール5家庭教師、見参ッ! 2次関数のコツ、成績アップ法を公開。X と y の変域から式を求める;
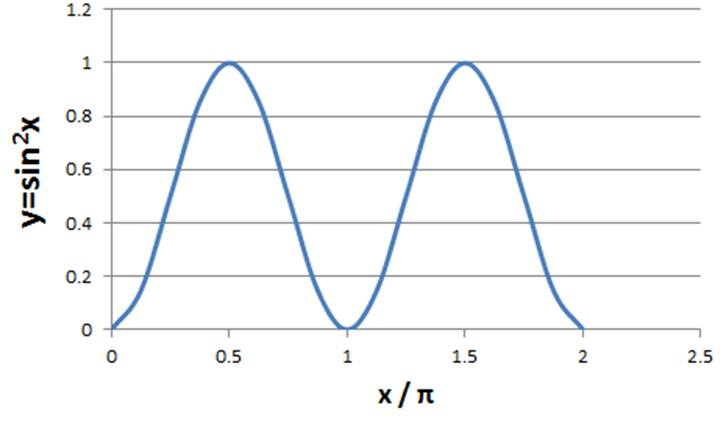
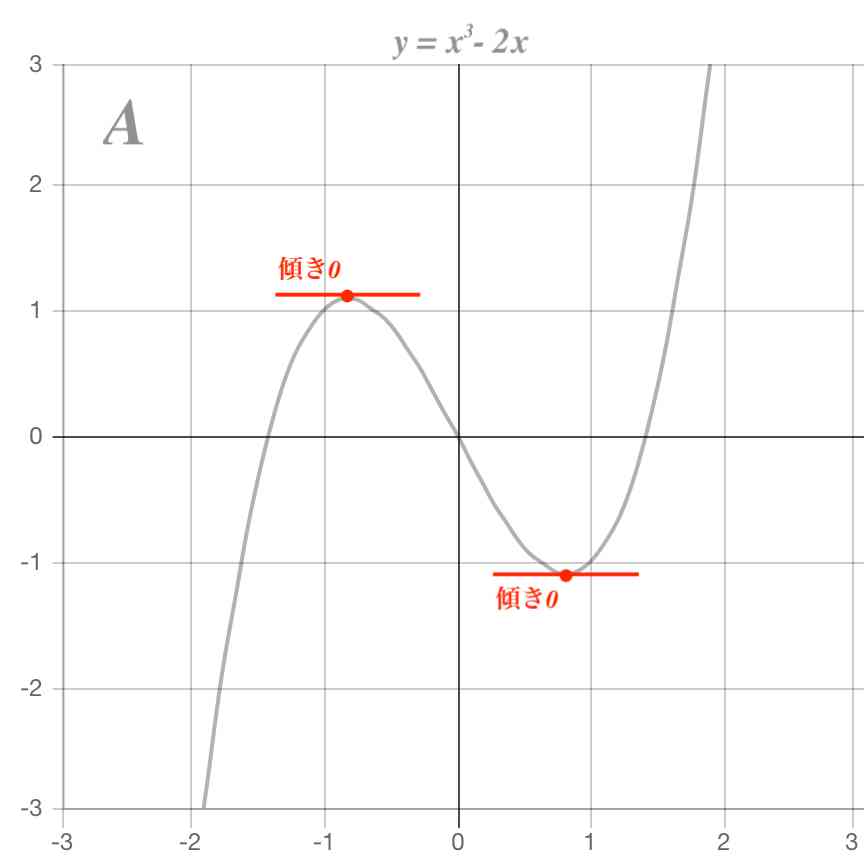
平方根・立方根・3分の2乗の説明 諫早湾の目次 本文に戻る グラフはいずれも,x を横軸,y を縦軸にとってあります.また,負(マイナス)の数は面倒になるので考えないことにします. 2乗と平方根文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R=(-∞,∞) で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。(y∛x²)²=1 ① で,♡を描きたいのでしょう. ①は陰関数ですが, dy/dx=0 という方程式の実数解を正確に求めることができなければ,増減の様子が分からず,微分法を用いてグラフを
Y=x2乗のグラフのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
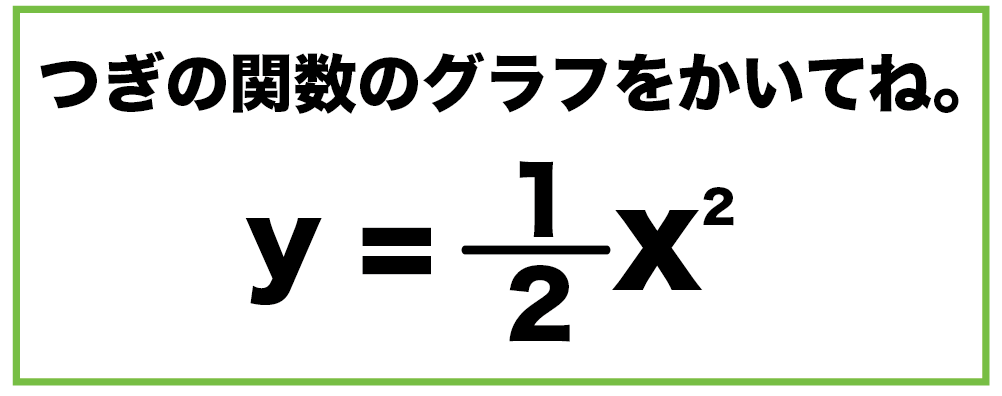 |  |  |
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 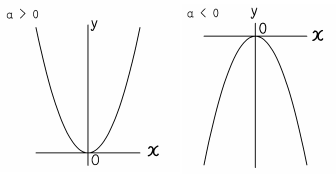 |  |
 |  | |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
「Y=x2乗のグラフ」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |
X2乗+ (y 3√x2乗)2乗=1 とありますが,3は係数ではなく 正しい式は x²指数関数 先ほど、 y = 2x y = 2 x のグラフを見ました。 このような、 y = ax y = a x という形をした関数を、 指数関数 (exponential function) と言います。 指数の部分に x x がある関数、ということですね。 なお、このとき、 a a には2つの条件が付きます。 1つは
コメント
コメントを投稿